hicFindTADs¶
Description¶
Uses a measure called TAD-separation score to identify the degree of separation between the left and right regions at each Hi-C matrix bin. This is done for a running window of different sizes. Then, TADs are called as those positions having a local TAD-separation score minimum. The TAD-separation score is measured using the z-score of the Hi-C matrix and is defined as the mean zscore of all the matrix contacts between the left and right regions (diamond). To find the TADs, the program needs to compute first the TAD scores at different window sizes. Then, the results of that computation are used to call the TADs. This is convenient to test different filtering criteria quickly as the demanding step is the computation of TAD-separation scores.
A simple example usage is:
$ hicFindTads -m hic_matrix.h5 –outPrefix TADs –correctForMultipleTesting fdr The bedgraph file produced by this tool can be used to plot the so-called insulation score along the genome or at specific regions. This score is much more reliable across samples than the number of TADs or the TADs width that can vary depending on the sequencing depth because of the lack of information at certain bins, and depending on the parameters used with this tool.
usage: hicFindTADs --matrix MATRIX --outPrefix OUTPREFIX
--correctForMultipleTesting {fdr,bonferroni,None}
[--minDepth INT bp] [--maxDepth INT bp] [--step INT bp]
[--TAD_sep_score_prefix TAD_SEP_SCORE_PREFIX]
[--thresholdComparisons THRESHOLDCOMPARISONS]
[--delta DELTA] [--minBoundaryDistance MINBOUNDARYDISTANCE]
[--chromosomes CHROMOSOMES [CHROMOSOMES ...]]
[--numberOfProcessors NUMBEROFPROCESSORS] [--help]
[--version]
Required arguments¶
- --matrix, -m
Corrected Hi-C matrix to use for the computations.
- --outPrefix
File prefix to save the resulting files: 1. <prefix>_tad_separation.bm The format of the output file is chrom start end TAD-sep1 TAD-sep2 TAD-sep3 .. etc. We call this format a bedgraph matrix and can be plotted using hicPlotTADs. Each of the TAD-separation scores in the file corresponds to a different window length starting from –minDepth to –maxDepth. 2. <prefix>_zscore_matrix.h5, the z-score matrix used for the computation of the TAD-separation score. 3. < prefix > _boundaries.bed, which contains the positions of boundaries. The genomic coordinates in this file correspond to the resolution used. Thus, for Hi-C bins of 10.000bp the boundary position is 10.000bp long. For restriction fragment matrices the boundary position varies depending on the fragment length at the boundary. 4. <prefix>_domains.bed contains the TADs positions. This is a non-overlapping set of genomic positions. 5. <prefix>_boundaries.gff Similar to the boundaries bed file but with extra information (p-value, delta). 6. <prefix>_score.bedgraph file contains the TAD-separation score measured at each Hi-C bin coordinate. Is useful to visualize in a genome browser. The delta and p-value settings are saved as part of the name.
- --correctForMultipleTesting
Possible choices: fdr, bonferroni, None
Select the bonferroni or false discovery rate for a multiple comparison. Bonferroni controls the family-wise error rate (FWER) and needs a p-value. The false discovery rate (FDR) controls the likelyhood of type I errors and needs a q-value. As a third option it is possible to not use a multiple comparison method at all (Default: “fdr”).
Default: “fdr”
Optional arguments¶
- --minDepth
Minimum window length (in bp) to be considered to the left and to the right of each Hi-C bin. This number should be at least 3 times as large as the bin size of the Hi-C matrix.
- --maxDepth
Maximum window length to be considered to the left and to the right of the cut point in bp. This number should around 6-10 times as large as the bin size of the Hi-C matrix.
- --step
Step size when moving from –minDepth to –maxDepth. Note, the step size grows exponentially as minDeph + (step * int(x)**1.5) for x in [0, 1, …] until it reaches maxDepth. For example, selecting step=10,000, minDepth=20,000 and maxDepth=150,000 will compute TAD-scores for window sizes: 20,000, 30,000, 40,000, 70,000 and 100,000
- --TAD_sep_score_prefix
Sometimes it is useful to change some of the parameters without recomputing the z-score matrix and the TAD-separation score. For this case, the prefix containing the TAD separation score and the z-score matrix can be given. If this option is given, new boundaries will be computed but the values of –minDepth, –maxDepth and –step will not be used.
- --thresholdComparisons
P-value threshold for the Bonferroni correction / q-value for FDR. The probability of a local minima to be a boundary is estimated by comparing the distribution (Wilcoxon ranksum) of the z-scores between the left and right regions (diamond) at the local minimum with the matrix z-scores for a diamond at –minDepth to the left and a diamond –minDepth to the right. If –correctForMultipleTesting is ‘None’ the threshold is applied on the raw p-values without any multiple testing correction. Set it to ‘1’ if no threshold should be used (Default: 0.01).
Default: 0.01
- --delta
Minimum threshold of the difference between the TAD-separation score of a putative boundary and the mean of the TAD-sep. score of surrounding bins. The delta value reduces spurious boundaries that are shallow, which usually occur at the center of large TADs when the TAD-sep. score is flat. Higher delta threshold values produce more conservative boundary estimations (Default: 0.01).
Default: 0.01
- --minBoundaryDistance
Minimum distance between boundaries (in bp). This parameter can be used to reduce spurious boundaries caused by noise.
- --chromosomes
Chromosomes and order in which the chromosomes should be plotted. This option overrides –region and –region2.
- --numberOfProcessors, -p
Number of processors to use (Default: 1).
Default: 1
- --version
show program’s version number and exit
Usage example¶
It is recommended to test multiple parameters of TAD calling with hicFindTADs before making conclusions about the number of TADs in a given sample or before comparing TAD calling between multiple conditions. In order to compare several TAD calling parameters at once, it is recommended to use hicPlotTADs.
Below you can find a typical command-line to use hicFindTADs:
$ hicFindTADs -m myHiCmatrix.h5 \
--outPrefix myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr \
--minDepth 3000 \
--maxDepth 31500 \
--step 1500 \
--thresholdComparisons 0.05 \
--delta 0.01 \
--correctForMultipleTesting fdr \
-p 64
This command will output the following files:
myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr_boundaries.bed
myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr_boundaries.gff
myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr_domains.bed
myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr_score.bedgraph
myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr_score.npz
myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr_tad_score.bm
myHiCmatrix_min3000_max31500_step1500_thres0.05_delta0.01_fdr_zscore_matrix.h5
TAD boundaries locations are stored in the boundaries files, domains.bed file contains the TAD locations, score files contain TAD separation score, or the so-called TAD insulation score, in various formats. As a side note, the tad_score.bm file is a bedgraph matrix that can be used to display TAD separation score curves in hicPlotTADs for example.
The zscore_matrix.h5 file contains a z-score matrix that is useful to quickly test the –thresholdComparisons, –delta and –correctForMultipleTesting parameters by using the –TAD_sep_score_prefix option pointing to this zscore_matrix.h5 file. For example to quickly test a –thresholdComparisons of 0.01 instead of 0.05 we can run the following command:
$ hicFindTADs -m myHiCmatrix.h5 \
--outPrefix myHiCmatrix_min10000_max40000_step1500_thres0.01_delta0.01_fdr \
--TAD_sep_score_prefix myHiCmatrix_min10000_max40000_step1500_thres0.05_delta0.01_fdr
--thresholdComparisons 0.01 \
--delta 0.01 \
--correctForMultipleTesting fdr \
-p 64
As you can see above, –minDepth, –maxDepth and –step are ignored because these parameters are used to calculate the z-score matrix which is here provided to –TAD_sep_score_prefix. Since z-score matrix computation is the most demanding step of hicFindTADs in terms of memory and computation, the above command will thus run significantly faster than the previous one.
Multiple combinations of parameters can be tested that way with only one z-score matrix computation. To compare several TAD calling outputs, we use hicPlotTADs with the following command using, for example, the following tracks.ini file:
command line:
$ hicPlotTADs --tracks tracks.ini --region chrX:6800000-8500000 -o TAD_calling_comparison.png
tracks.ini:
[x-axis]
fontsize=10
[hic]
file = myHiCmatrix.h5
title = Threshold 0.05
colormap = Spectral_r
depth = 400000
min_value = 1
max_value = 80
transform = log1p
file_type = hic_matrix
show_masked_bins = false
[tads]
file = myHiCmatrix_min10000_max40000_step1500_thres0.05_delta0.01_fdr_domains.bed
file_type = domains
border_color = black
color = none
overlay_previous = share-y
[hic]
file = myHiCmatrix.h5
title = Threshold 0.01
colormap = Spectral_r
depth = 400000
min_value = 1
max_value = 80
transform = log1p
file_type = hic_matrix
show_masked_bins = false
[tads]
file = myHiCmatrix_min10000_max40000_step1500_thres0.01_delta0.01_fdr_domains.bed
file_type = domains
border_color = black
color = none
overlay_previous = share-y
[spacer]
height = 0.1
[hic]
file = myHiCmatrix.h5
title = Threshold 0.005
colormap = Spectral_r
depth = 400000
min_value = 1
max_value = 80
transform = log1p
file_type = hic_matrix
show_masked_bins = false
[tads]
file = myHiCmatrix_min10000_max40000_step1500_thres0.005_delta0.01_fdr_domains.bed
file_type = domains
border_color = black
color = none
overlay_previous = share-y
[spacer]
height = 0.1
[hic]
file = myHiCmatrix.h5
title = Threshold 0.001
colormap = Spectral_r
depth = 400000
min_value = 1
max_value = 80
transform = log1p
file_type = hic_matrix
show_masked_bins = false
[tads]
file = myHiCmatrix_min10000_max40000_step1500_thres0.001_delta0.01_fdr_domains.bed
file_type = domains
border_color = black
color = none
overlay_previous = share-y
[spacer]
height = 0.1
[bigwig]
file = /data/processing/ChIP-Seq_Embryos/H3K36me3_14c.bigwig
title = H3K36me3
color = darkred
min_value = 0
max_value = auto
height = 2
file_type = bigwig
[spacer]
height = 0.1
[genes]
file = /data/group/bedfiles/dm6/genes_sorted.bed
title = genes
color = black
height = 18
labels = true
file_type = bed
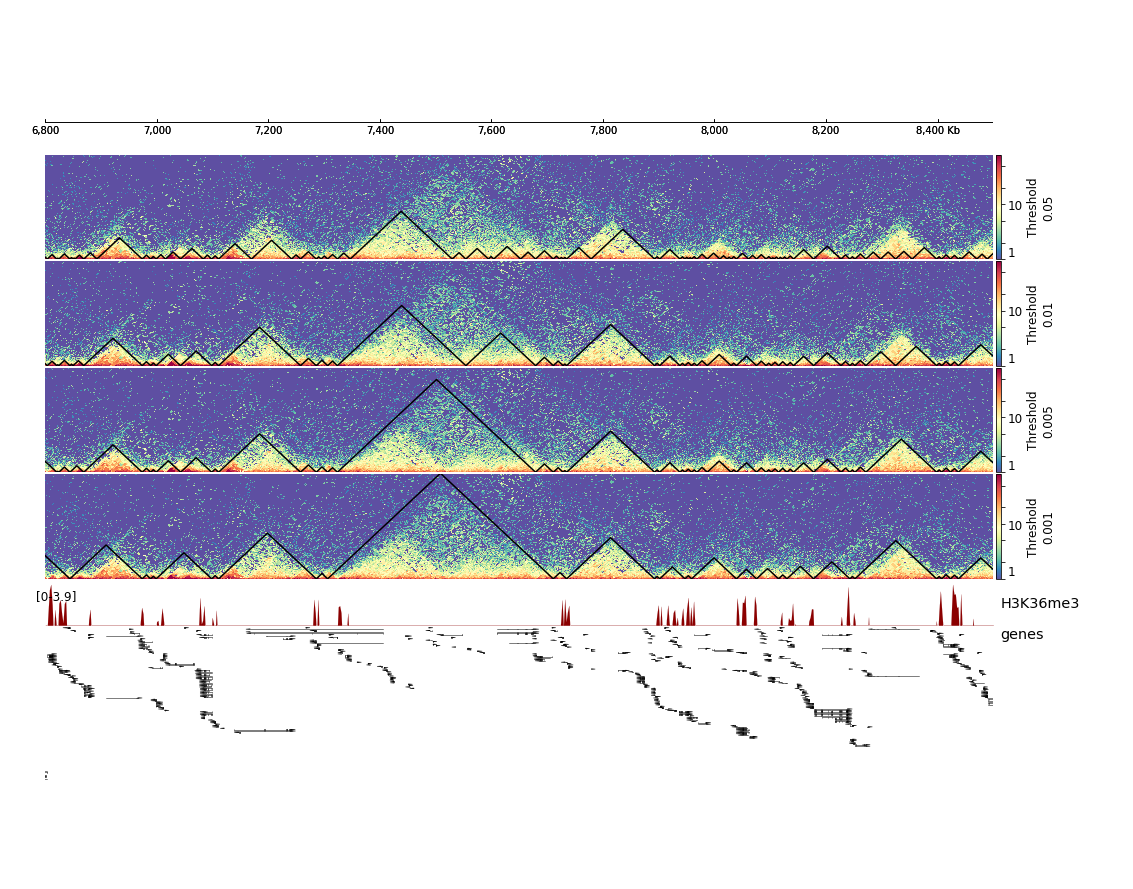
This will result in the following plot where we see that the fourth set of hicFindTADs parameters with a threshold of 0.001 gives the best results in terms of TAD calling compared to the corrected Hi-C counts distribution and compared to the enrichment of H3K36me3, which is known to be enriched at TAD boundaries in Drosophila melanogaster.
Notes¶
In the _domains.bed output file, the 5th column contains the TAD-separation score at the boundary located at the start of each domain.
The process to identify boundaries is as follows:
call all local minima in the average TAD-score. Each local minimum should be separated by at least min_boundary_distance. If this value is not given, it is set to the average bin size * 4
for each local minimum detected, compute its p-value and then compute a q-value.
for each local minimum detected, compute the ‘delta’ which is the difference between the mean TAD-score of the 10 bins before and the 10 bins after the minimum (excluding the min point)
keep only those minima that fulfill the following criteria: the p-value (or q-value depending on the user selection) should be below the given threshold and the delta should be above the user defined threshold
everything between 2 consecutive boundaries is a TAD
For computation of the p-values, the distribution of the z-scores at the ‘diamond’ above the local minimum is compared with the distribution of z-scores that are min_depth downstream using the Wilcoxon rank-sum test. Similarly, the distribution of z-scores is computed with the z-scores min_depth upstream of the local minimum. The smallest of the two p-values is assigned to the local minimum.
If min_depth is not given, this is computed as bin size * 30 (if the bins are smaller than 1000), as bin size * 10 if the bins are between 1000 and 20.000 and as bin size * 5 if the bin size is bigger than 20.000.
If max_depth is not given, this is computed as bin size * 60 (if the bins are smaller than 1000), as bin size * 40 if the bins are between 1000 and 20.000 and as bin size * 10 if the bin size is bigger than 20.000.