hicTransform¶
Converts the (interaction) matrix to different types of obs/exp, pearson or covariance matrix.
usage: hicTransform --matrix MATRIX --outFileName OUTFILENAME
[--method {obs_exp,obs_exp_lieberman,obs_exp_non_zero,pearson,covariance}]
[--ligation_factor]
[--chromosomes CHROMOSOMES [CHROMOSOMES ...]]
[--perChromosome] [--help] [--version]
Required arguments¶
- --matrix, -m
input file. The computation is done per chromosome.
- --outFileName, -o
File name to save the exported matrix.
Optional arguments¶
- --method, -me
Possible choices: obs_exp, obs_exp_lieberman, obs_exp_non_zero, pearson, covariance
Transformation methods to use for input matrix. Transformation is computed per chromosome.obs_exp computes the expected matrix as the sum per genomic distance j divided by maximal possible contacts: sum(diagonal(j) / number of elements in diagonal(j) obs_exp_lieberman computes the expected matrix as the sum per genomic distance j divided by the : sum(diagonal(j) / (length of chromosome - j))obs_exp_non_zero computes the expected matrix as the sum per genomic distance j divided by sum of non-zero contacts: sum(diagonal(j) / number of non-zero elements in diagonal(j)Optionally, ``–ligation_factor` can be used for this method as has been used by HOMER software. If –ligation_factor, then exp_i,j = exp_i,j * sum(row(i)) * sum(row(j)) / sum(matrix)pearson computes the Pearson correlation of the input matrix: Pearson_i,j = C_i,j / sqrt(C_i,i * C_j,j) and C is the covariance matrixcovariance computes the Covariance of the input matrix: Cov_i,j = E[M_i, M_j] - my_i * my_j where M is the input matrix and my the mean (Default: “obs_exp”).
Default: “obs_exp”
- --ligation_factor
Setting this flag, multiplies a scaling factor to each entry of the expected matrix to take care of the proximity ligation as has been explained in Homer software. This flag is only affective with obs_exp_non_zero method and will be ignored if any other obs/exp method is chosen.
Default: False
- --chromosomes
List of chromosomes to be included in the computation.
- --perChromosome, -pc
Each chromosome is processed individually, inter-chromosomal interactions are ignored. Option not valid for obs_exp_lieberman.
Default: False
- --version
show program’s version number and exit
Background¶
hicTransform transforms a given input matrix into a new matrix using one of the following methods:
obs_exp
obs_exp_lieberman
obs_exp_non_zero
pearson
covariance
All expected values are computed per genomic distances.
Usage¶
$ hicTransform -m matrix.cool --method obs_exp -o obs_exp.cool
For all images data from Rao 2014 was used.
Observed / Expected¶
All values, including non-zero values, are used to compute the expected values per genomic distance.
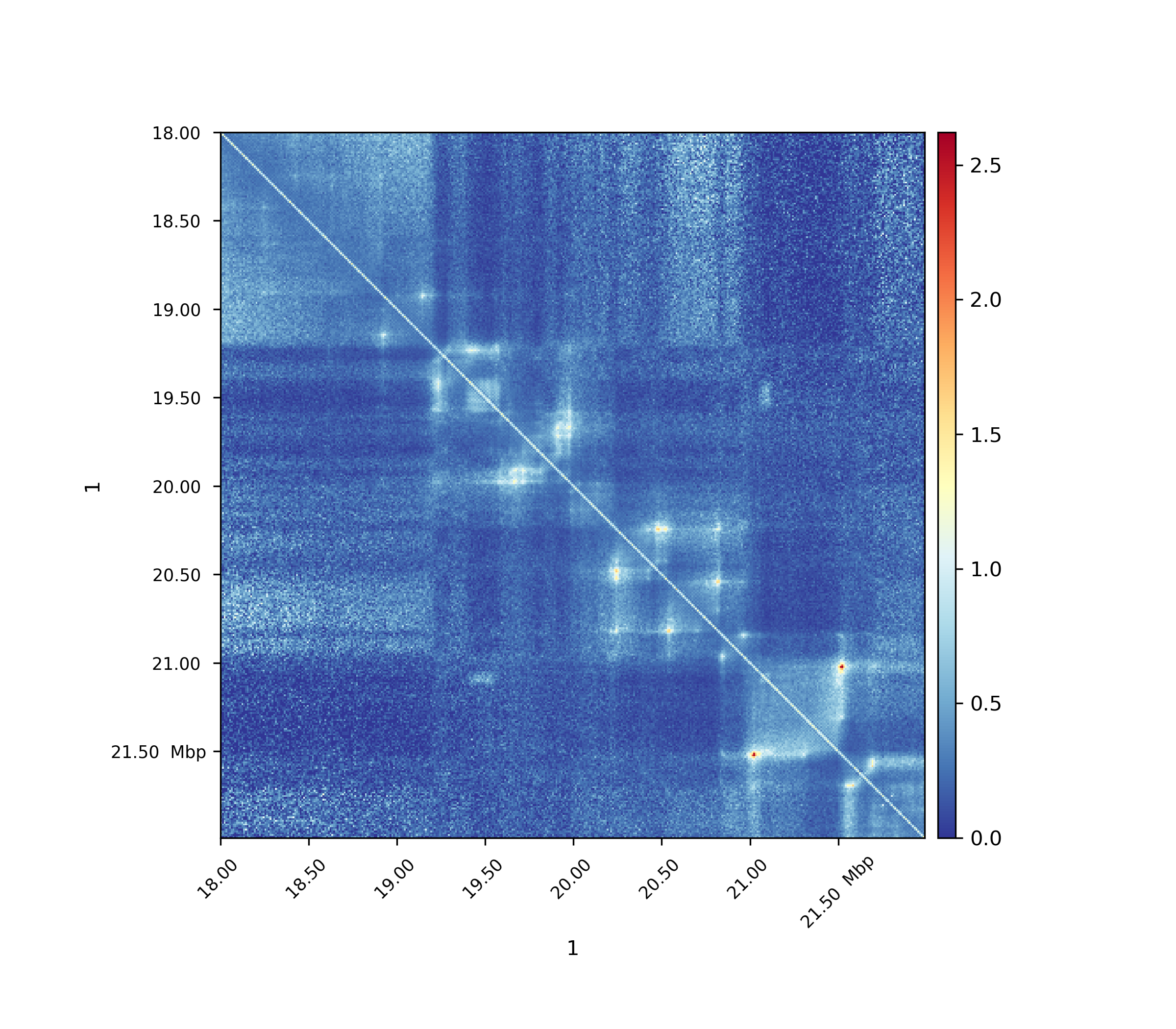
Observed / Expected lieberman¶
The expected matrix is computed in the way as Lieberman-Aiden used it in the 2009 publication. It is quite similar to the obs/exp matrix computation.
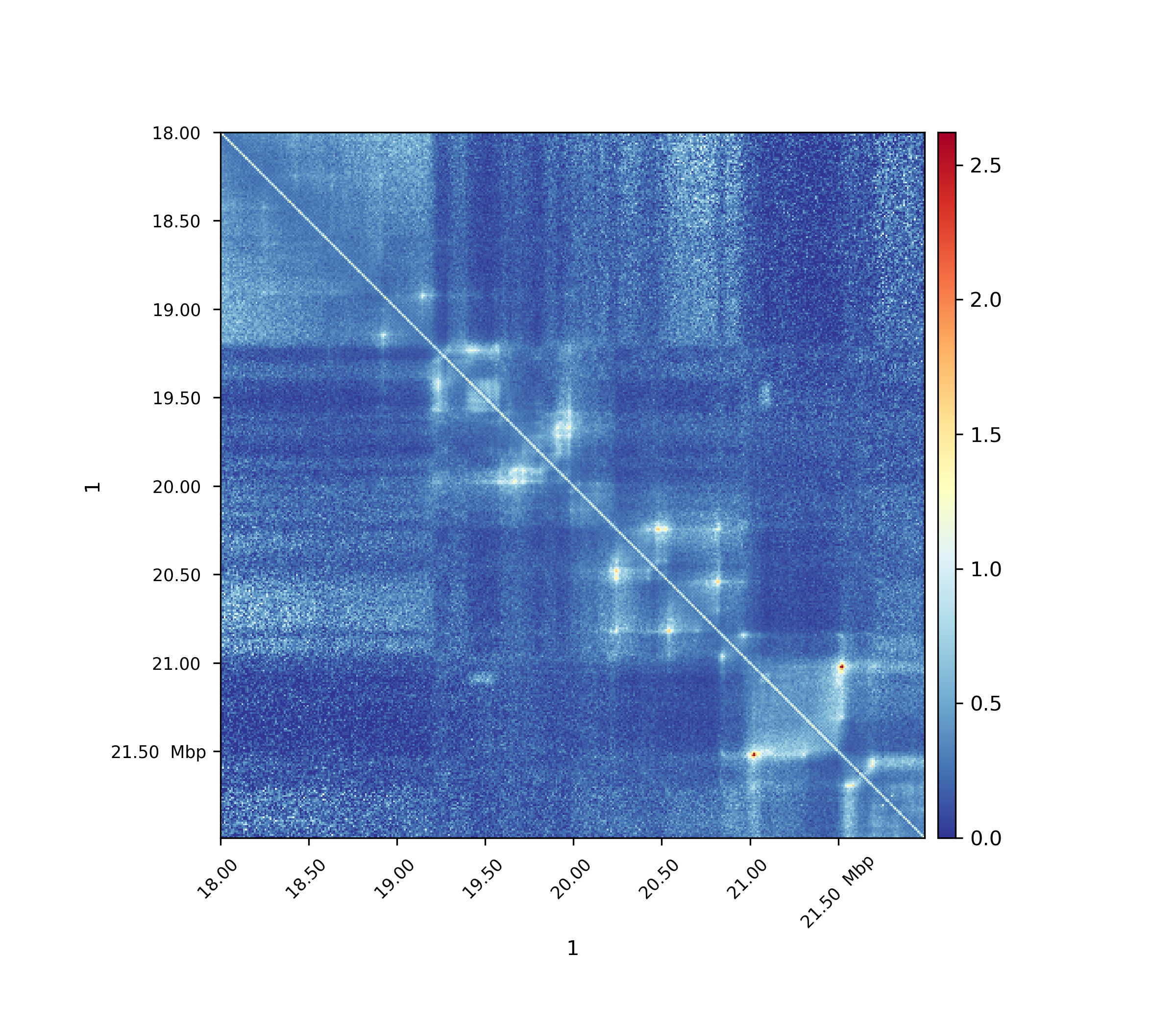
Observed / Expected non zero¶
Only non-zero values are used to compute the expected values per genomic distance, i.e. only non-zero values are taken into account for the denominator.
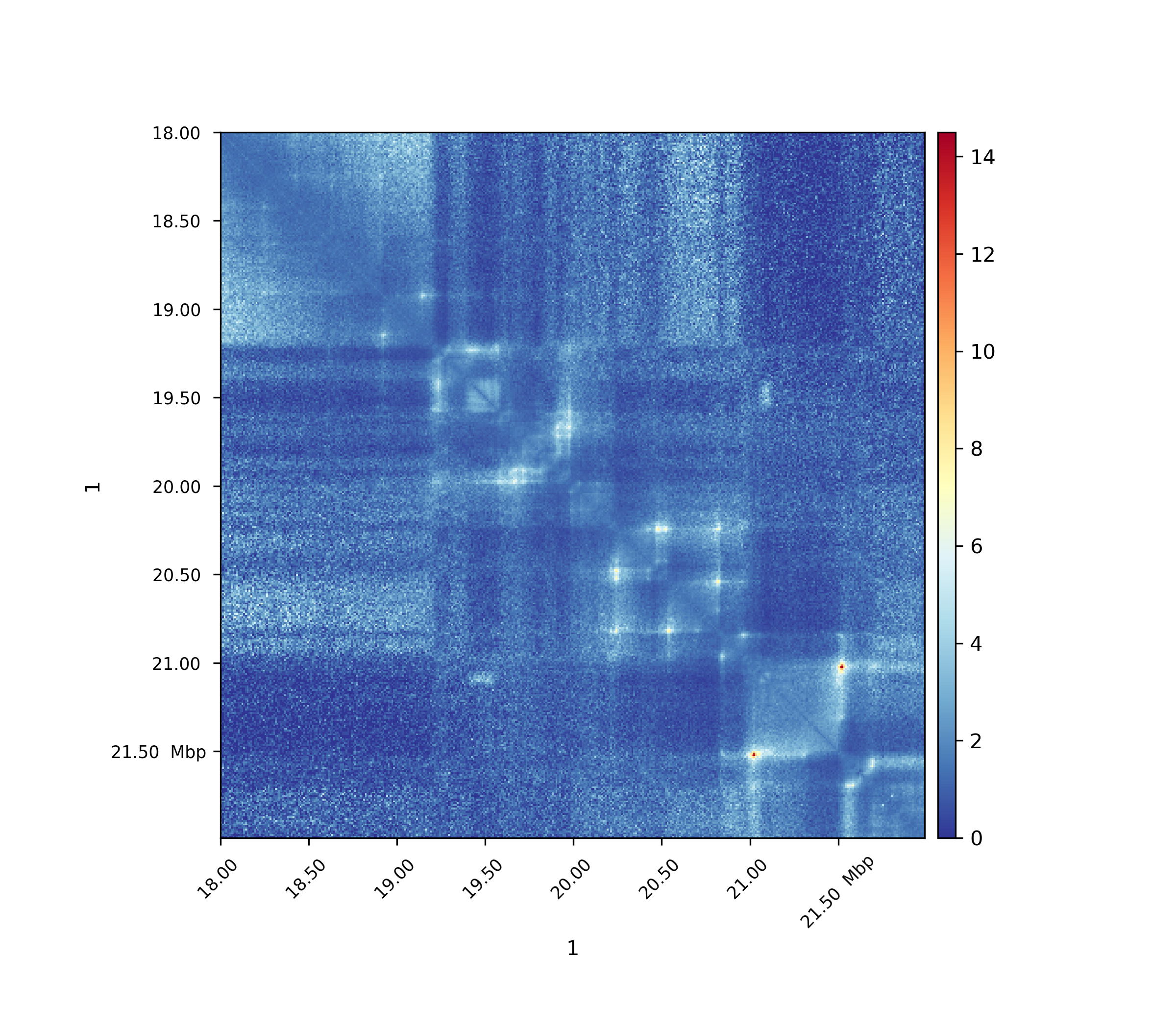
By adding the –ligation_factor flag, the expected matrix can be re-scaled in the same way as has been done by Homer software when computing observed/expected matrices with the option ‘-norm’.

Pearson correlation matrix¶
C is the covariance matrix
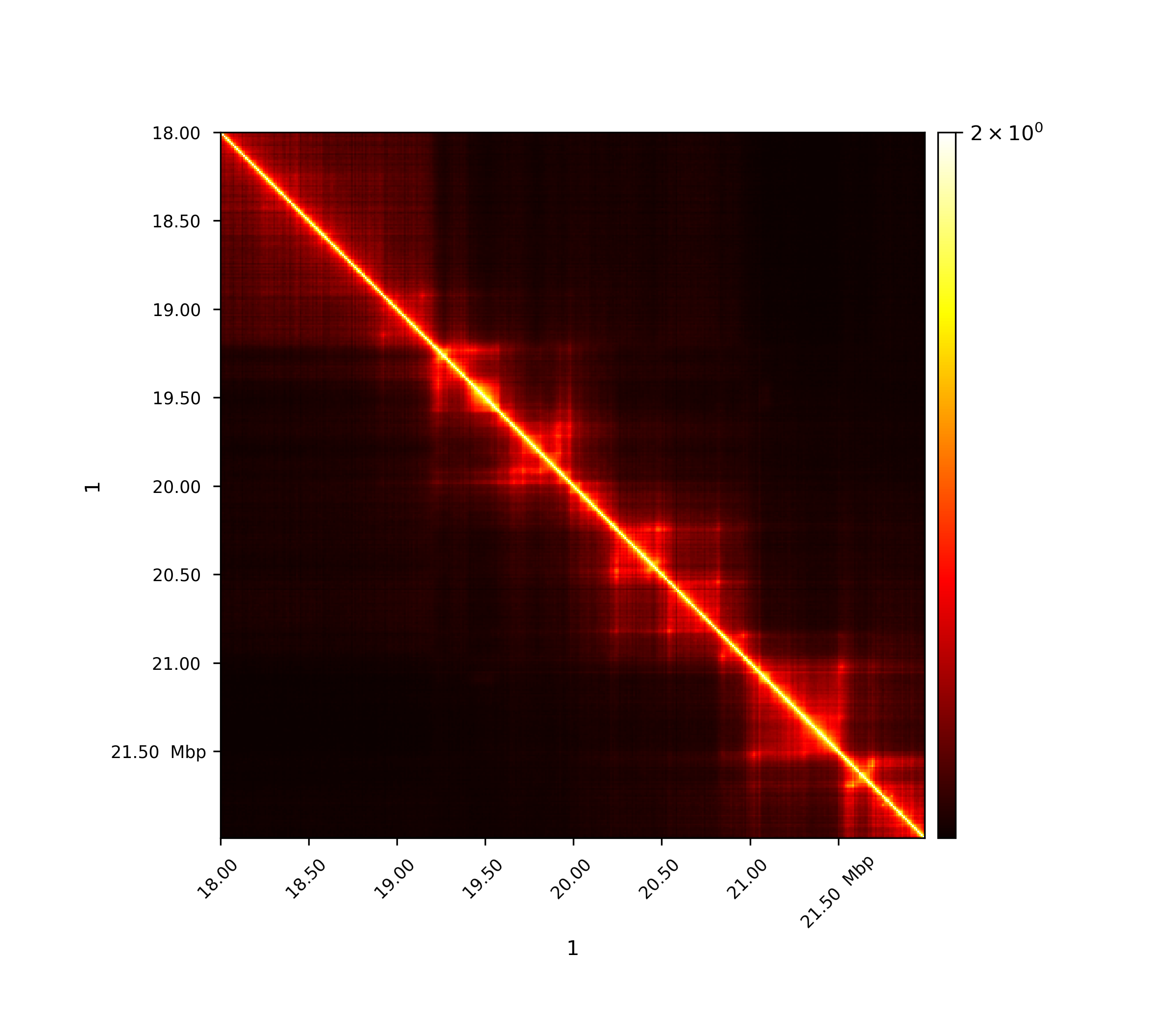
The first image shows the Pearson correlation on the original interaction matrix, the second one shows the Person correlation matrix on an observed/expected matrix. A consecutive computation like this is used in the A/B compartment computation.
Covariance matrix¶
where M is the input matrix and \(\mu\) the mean.